When it comes to trigonometry, knowing the unit circle is key. I think these three things will be very helpful.
Part 1: Derive the values of two triangles
The triangles that are part of unit circle are 45-45-90 triangle and 30-60-90 triangle. These two triangles are what make up all the values on the unit circle except the points on the axis's (i.e. 0, 90, 180, 270, 360). Let's derive the values from these two triangles.
45-45-90 Triangle
Since it is an isosceles, I write with the legs equaling to x and the hypotenuse equal to 1 (see figure 1).
Figure 1. 45-45-90 Triangle.
30-60-90 Triangle
With the 30-60-90 triangle, I can take two of these triangles and for an equilateral triangle (see figure 2).
Figure 2. Equilateral triangle with two 30-60-90 triangles
Now I can find the remaining side of the 30-60-90 triangle.
Part 2: Values that appear in the unit circle.
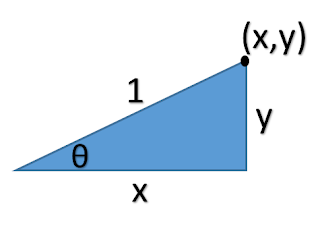
The unit circle is formed by a right triangle (see figure 3). The angle of focus is formed by the horizontal side and the hypotenuse of the right triangle.
Figure 3. Right triangle in Unit Circle
The trigonometric functions can be formed using the coordinates.
This means that the signs of the ratios are based the location of the point on the unit circle. In other words, it depends which quadrant the point is in. Now consider the signs in each quadrant. In quadrant I, the
points (x,y) are (+,+). This means all trigonometric functions are positive in
quadrant I. In quadrant II, the points are (-,+). So, sine function is positive
because the y’s are positive, but the other functions are negative. In quadrant
III, the points are (-,-), so the tangent function would be positive, but the
sine and cosine function would result in a negative. In the quadrant IV, the
points are (+,-). Cosine function would be positive, but the others would be
negative.
An easy way to remember the signs rules is with the acronym, A Smart Trig Class. It is an order of the quadrants.
Figure 4. A Smart Trig Class with Quadrants
It signifies which values are positive.
In the first quadrant, the values of ALL trigonometric functions are positive.
In the second quadrant, the values of the SINE function are positive and the
others are negative. In the third quadrant, the values of the TANGENT function
are positive and the others are negative. In the fourth quadrant, the values of
the COSINE function are positive and the others are negative.
Hopefully, these patterns are helpful for the unit circle. I
think the patterns are useful, because it makes the memory work easier. And if
you forget, you can always use the patterns to make your own unit circle.
