Let's talk about a variance being negative. The other day I worked out a discrete probability
distribution problem, and I got a negative variance. The variance is always
positive. It would be zero if the data was all the same value. It should never
be negative.
In this post, I will show how I first did the problem.
Then I’ll show why that the negative answer is incorrect, and how it happened.
Problem
Calls for a crisis hotline. The number of calls received per
day at a crisis hotline is distributed as follows:
|
Number X
|
30
|
31
|
32
|
33
|
34
|
|
Probability P(x)
|
0.05
|
0.21
|
0.38
|
0.25
|
0.11
|
Find the mean, variance, and the standard deviation of the
distribution.
(Problem #18 pg. 307 from Bluman, A. (2013). Elementary statistics (9th ed). New York, NY: McGraw-Hill)
Part 1: The work at first glance
Finding the mean
The mean is 32.2 using the rounding rule. This is correct.
Finding the variance
Obviously,
you can’t get a negative variance, so I tried the exact mean, 32.16.
1.1 is the correct variance using the
rounding rules.
Part 2: Finding the
Error
The work is correct. It should not matter if you plug in
the rounded or exact mean. The variance should still be positive. The issue
comes up with the shortcut formula. When the regular formula is used for
variance, it results in variance close to 1.0744 using the rounded mean, 32.2.
Note: the differences are always being
squared resulting in either a zero or positive value. They are never negative.
Because of this, variance is always positive. It should not matter if 32.16 or
32.2, but it does.
Using the regular formula with the rounded mean, it is
pretty close to the variance using the exact mean. Here is the regular formula
for variance using the exact mean:
It is the same as the shortcut formula as it should be.
Notice with using the exact mean or the rounded mean, you still get 1.1 for
your variance when using the rounding rules. But why is it when you use the
rounded mean for the shortcut and regular formula you get two different answers
with one being negative.
It is important here to look at how the shortcut formula is
derived from the regular formula. Note that µ is a constant in the formula.
The problem arises with the substitution. In order to make
the substitution and combine like-terms, you are assuming that all µ’s are the
same. If you use the rounded mean, the µ’s are not all the same. You will have
unlike terms, so you will not able to combine them to simplify.
Notice the solution is the same one we found using the
regular formula.
Conclusion
When you using the shortcut formula for
calculating the variance for a discrete probability distribution, you have to
be careful when you plug in a rounded mean. It is better to use the exact mean if
possible, or to use a rounded mean closer to the exact. The question arises from this, “Does this happen with other shortcut
formulas found in statistics?”
In case, if you worrying how to get the standard deviation, you just need to take the square root of the variance. By the way, variance should always be positive or equal to zero.



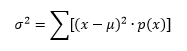








No comments:
Post a Comment