A Proof for Pythagorean Theorem

Let's talk Pythagorean Theorem.

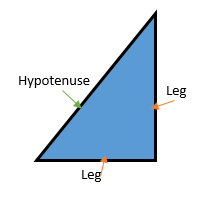
One of my favorite proofs for Pythagorean Theorem is pictorial. Pythagoras, the geometer, and his students discovered the pattern that sum of squares of the legs equals the square of the hypotenuse.  The legs are the sides of a right triangle; they are adjacent (next to) the right angle of the right triangle. The hypotenuse is the side of the right triangle opposite of the right angle (see figure 1).

Figure 1. Diagram of parts of right triangle.

Pythagorean Theorem is better known as a²+b²=c². Now let me show you the pictorial proof. I’ll start with a large square with sides, a+b. Within the large square, there are four right triangles with sides a,b, and c where a and b are legs and c is the hypotenuse (see figure 2).

 

Figure 2. Square with right triangles.

Now I will calculate area of each of the shapes (see figure 3). The area of a triangle is one half base times height. The area of a square is one side squared.

 

Figure 3. Square with areas.

We know that the sum of the parts equal the area of the whole, so:

Therefore,

a²+b²=c².

If you got math questions, e-mail at jdmathguy@gmail.com. Let's talk math.