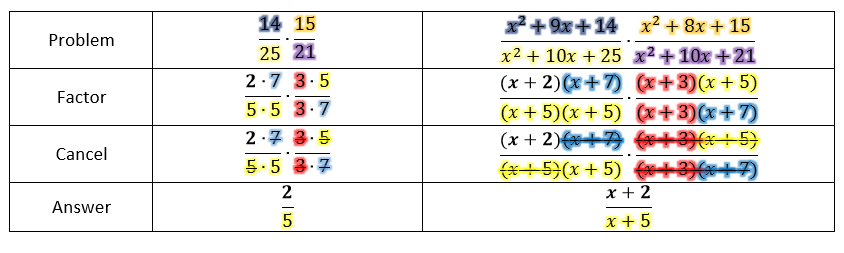
Let's talk about factoring polynomials. The method I'm going to show you is almost universal. It is a combination of the product-sum method, OI method, and the box method. This method of factoring can factor 2 terms (difference of squares), 3 terms (A=1), 3 terms (A doesn't =1), and 4 terms.
I call this method of factoring, the OI-box method. It is a variation on the OI method. If you are curious about the OI method, check out my recent YouTube video:
OI method. It uses the Outer and Inner of FOIL. This method does the same. I'll explain the steps of the method first. Second, I will show a flowchart related to the method. Then I will show you some examples.
1. The Steps of Method
Step 1: Identify the number of terms and type.
Step 2: Apply the product-sum if necessary.
- Set-up. Put AC on the top and B on the bottom.
- Find the left and the right by asking two
questions
- What product equals AC?
- What sum equals B
Step 3: Apply the OI-box method. The
solutions found in step 2 are the outer and inner or the O-I in FOIL.
- Set-up. Rows as O-I and Columns as F-L in FOIL
- Find the squares either by GCF of row and column
or missing factor within a row or column.
- If needed, put negative only in the L-column.
Step 4: Take the diagonals found in step 3 and use them as
factors.
Note: For trinomials (Ax2+Bx+C), they
are factorable when B2-4AC equals a square (i.e. 0, 1,4,9,...). If not, it is prime.
2. Flowchart of the Method
3. 5 Examples using the Method
A. Factor polynomial with 4 terms
B. Factor trinomial (3 terms) with A equals 1
C. Factor trinomial (3 terms) with A doesn't equal 1
D. Factor perfect square trinomial (3 terms)
E. Factor a difference of squares (2 terms)
A. Example 1
B. Example 2
C. Example 3
D. Example 4
E. Example 5
Conclusion
For
a method of factoring, it covers a wide variety of scenarios. The method cannot
be used with a difference or sum of cubes, or when you have a difference of
squares with 4 terms. Nonetheless this method of factoring can be very useful.
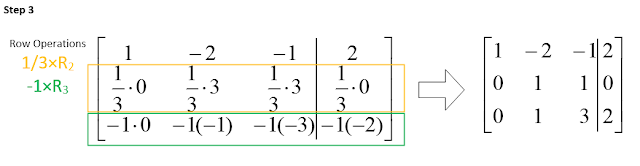



 Example 2: Solve using
Gauss-Jordan Elimination
Example 2: Solve using
Gauss-Jordan Elimination