System of Equations and Matrices

Let's talk about solving a system of equations using matrices, specifically Gaussian Elimination and Gauss-Jordan Elimination. In the first example, I will show the "in-between" steps using the row transformations. In the second example, I will not show the "in-between" steps, use the Gauss-Jordan Elimination method. Also it will a system of 4 equations with 4 unknowns.

Example 1: Solve using Gaussian Elimination

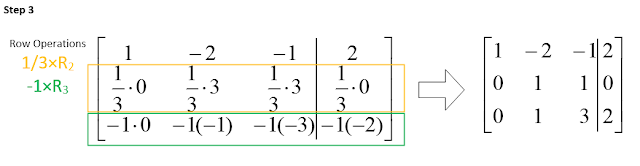
If you are able, always check your answer by plugging in what you found. If it is true for all, then it is a solution.


Example 2: Solve using Gauss-Jordan Elimination

First, convert the system of equations to a matrix. Then with each step, apply the row transformations. With the Gauss-Jordan method, you want to keep going until you get the identity matrix on the left-hand side. The identity matrix has a diagonal of 1's and the rest are zeroes. Gauss-Jordan Elimination is like Gaussian Elimination, but it goes a little further.

For more on matrices, check out my youtube channel. If you have any questions or blog ideas, you can e-mail me at jdmathguy@gmail.com